Trading is all about forecasting price. If you have been reading my Forex Strategies 2.0 Blog, you must have seen I am focusing more and more on algorithmic trading. If you can forecast currency pair price with a reasonable degree of accuracy, you can make a lot of pips. Markets have changed a lot. Today algorithms rule the market. Wall Street is being ruled by algorithmic trading systems. Big banks and hedge funds have developed their own algorithmic trading systems that don’t need any human intervention at all. Facebook Core Data Science Team released it’s Prophet for public in March of this year. Facebook has been using this algorithm extensively for making reliable forecasting for planning and goal setting. Prophet is a method for forecasting time series data. It is a robust algorithm which uses the standard General Additive Models to model non linear time series. Prophet can deal with missing data, big outliers and shifts in trends. When we are forecasting currency prices we are forecasting financial time series. Currency prices suddenly change direction meaning currency prices have lot of shits in trends. In this post I am going to discuss how we can use Facebook’s Prophet Algorithm in forex trading. Did you read the post that explains why high frequency returns are not normally distributed?
Facebook Prophet Algorithm is available in both R and Python. R and Python are two powerful machine learning languages that you should learn and master if you want to become an algorithmic trader. In this post we will be using R. Installing Prophet package is easy. Making forecasts with Prophet is pretty fast. Time taken is less than 1 second. This serves our purpose if we are trading high frequency data. Behind the scene this algorithm uses Stan. We don’t need to bother about Stan. Stan is used in Bayesian analysis. Using the algorithm in R is easy so don;’t worry at all what is Stan. First I want to discuss Prophet Algorithm in some detail so that we know how it models the time series. Prophet works best for daily data this is what the Core Data Science team says. So we will start off with daily data and in the end check if we can use this algorithm on high frequency data like 1 minute. Did you read the post on how to use Echo State Networks in forex trading?
Currency pair time series is known generally as financial time series. All financial markets have something in common. All financial markets are highly stochastic in nature and predicting a financial time series is a challenging task. A lot of research has been carried out but still it is very difficult to predict a financial time series. Let’s discuss GBPUSD daily time series. GBPUSD daily time series can change direction suddenly. We can break GBPUSD daily time series into 4 components:
- Growth function to model non periodic changes. For example FOMC Meeting announces rate hike. This suddenly forces GBPUSD daily price to soar high rapidly. We can model it as a growth function. Now you should keep this in mind, financial time series behaves differently when price rises and very differently when price falls. Price falls very rapidly as compared to when it rises. I think we can model this as a growth function.
- The second component that break the financial time series is the weekly seasonality. I don’t think we need to model monthly and yearly seasonality. We should keep Occam’s Razor that stipulates that we should keep the model as simple as possible.
- We need to have a model regarding holidays. Holidays can shock the market big time. As a currency trader I know a lot of things can happen over the weekend when the market is closed. On Sunday there can be some political statement that can move the market big time. For example, UK Prime Minister announced general elections over Sunday, On Monday, GBPUSD opened with a big gap. So we need to model the holidays as a separate component.
- An error term to model idiosyncratic changes that are missed by our model. We will assume that the error terms are normally distributed.
Sounds complicated? Good news! We don’t have to do anything. Prophet algorithm will do everything for us automatically. As said above, this algorithm uses Stan behind the scene which is a Bayesian algorithm. Everything is done automatically so we don’t have to worry a lot if we are getting good predictions. First we will let this algorithm make the prediction. If the prediction is not good, we can then tweak it to make the prediction more accurate. Let’s hope Prophet makes our life easy. We will have to check. Let’s start then. First read this post on a random walk with GBPUSD. In this post I show how we can use an auto-regressive model for predicting GBPUSD prices.
Keep this in mind. Forex trading is all about correctly predicting the price. You don’t need to be 100% accurate. If you can predict the market direction you can reduce your losing trades by 50%. In the past few years, trading has become very very algorithmic. Today algorithms rule the market. Below is the R code to implement the Prophet algorithm.
> library("prophet") Loading required package: Rcpp > library("readr") > data <- read_csv("D:/MarketData/EURUSD+1440.csv", + col_names=c("Date", "Time", "Open", "High", + "Low", "Close", "Volume"), + col_types=cols(Date=col_date(format='%Y.%m.%d'))) > x1 <-nrow(data) > data <- data[, -2] > data1 <- data[(x1-400):(x1-35),] > df1 <- data1[, c(1,5)] > head(df1) # A tibble: 6 × 2 Date Close <date> <dbl> 1 2015-11-10 1.07241 2 2015-11-11 1.07440 3 2015-11-12 1.08137 4 2015-11-13 1.07492 5 2015-11-16 1.06863 6 2015-11-17 1.06424 > tail(df1) # A tibble: 6 × 2 Date Close <date> <dbl> 1 2017-03-31 1.06581 2 2017-04-03 1.06686 3 2017-04-04 1.06725 4 2017-04-05 1.06625 5 2017-04-06 1.06435 6 2017-04-07 1.05958 > colnames(df1) <- c("ds", "y") > m1 <- prophet(df1) STAN OPTIMIZATION COMMAND (LBFGS) init = user save_iterations = 1 init_alpha = 0.001 tol_obj = 1e-012 tol_grad = 1e-008 tol_param = 1e-008 tol_rel_obj = 10000 tol_rel_grad = 1e+007 history_size = 5 seed = 291079117 initial log joint probability = -2.24128 Optimization terminated normally: Convergence detected: relative gradient magnitude is below tolerance > str(m1) List of 18 $ growth : chr "linear" $ changepoints : Date[1:25], format: "2015-11-26" "2015-12-11" "2015-12-30" ... $ n.changepoints : num 25 $ yearly.seasonality : logi TRUE $ weekly.seasonality : logi TRUE $ holidays : NULL $ seasonality.prior.scale: num 10 $ changepoint.prior.scale: num 0.05 $ holidays.prior.scale : num 10 $ mcmc.samples : num 0 $ interval.width : num 0.8 $ uncertainty.samples : num 1000 $ start : Date[1:1], format: "2015-11-10" $ end : Date[1:1], format: "2017-04-07" $ y.scale : num 1.15 $ stan.fit : NULL $ params :List of 6 ..$ k : num 0.24 ..$ m : num 0.947 ..$ delta : num [1, 1:25] -2.21e-08 -2.77e-01 -1.27e-01 1.14e-01 8.74e-02 ... ..$ sigma_obs: num 0.00647 ..$ beta : num [1, 1:27] 0 0.01132 -0.01187 0.00207 -0.00951 ... ..$ gamma : num [1:25(1d)] 6.88e-10 1.67e-02 1.23e-02 -1.53e-02 -1.43e-02 ... $ history :Classes ‘tbl_df’, ‘tbl’ and 'data.frame': 366 obs. of 4 variables: ..$ ds : Date[1:366], format: "2015-11-10" "2015-11-11" "2015-11-12" ... ..$ y : num [1:366] 1.07 1.07 1.08 1.07 1.07 ... ..$ t : num [1:366] 0 0.00195 0.00389 0.00584 0.01167 ... ..$ y_scaled: num [1:366] 0.93 0.932 0.938 0.932 0.927 ... - attr(*, "class")= chr [1:2] "list" "prophet" > future <- make_future_dataframe(m1, periods = 35) > tail(future) ds 395 2017-05-06 396 2017-05-07 397 2017-05-08 398 2017-05-09 399 2017-05-10 400 2017-05-11 > forecast1 <- prophet:::predict.prophet(m1, future) > plot(m1, forecast1) > prophet_plot_components(m1, forecast1)
We have used the daily data. If you read the Facebook documentation for Prophet Algorithm, it says it works best for daily data. Now this algorithm makes the forecasting automatically. Take a plot of the forecast.
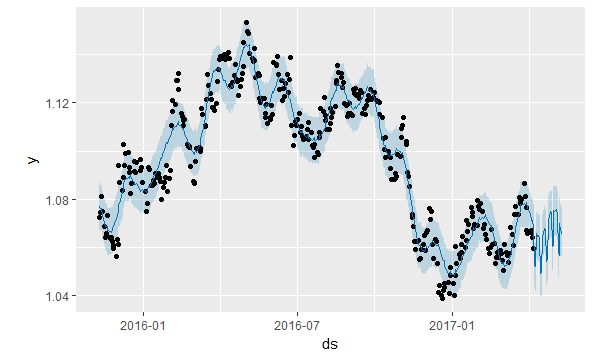
Above you can see the plot of the forecast with the tolerance levels. Prophet gives you the higher and lower tolerance levels of the forecast as well. We can also decompose the above plot into the trend, weekly seasonality and the yearly seasonality.
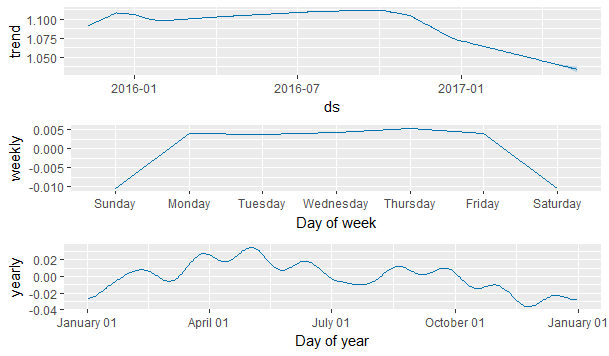
Below is the forecast made in tabular form.
> tail(forecast1, 35) ds t trend yhat_lower yhat_upper trend_lower trend_upper 366 2017-04-07 1.000000 1.043909 1.058503 1.078211 1.043909 1.043909 367 2017-04-08 1.001946 1.043621 1.043833 1.062444 1.043621 1.043621 368 2017-04-09 1.003891 1.043332 1.041914 1.061872 1.043332 1.043332 369 2017-04-10 1.005837 1.043043 1.055876 1.075024 1.043043 1.043043 370 2017-04-11 1.007782 1.042754 1.055409 1.073975 1.042754 1.042754 371 2017-04-12 1.009728 1.042465 1.054134 1.074271 1.042456 1.042487 372 2017-04-13 1.011673 1.042177 1.054888 1.074283 1.042117 1.042242 373 2017-04-14 1.013619 1.041888 1.054295 1.073646 1.041768 1.041996 374 2017-04-15 1.015564 1.041599 1.039399 1.058453 1.041402 1.041760 375 2017-04-16 1.017510 1.041310 1.039957 1.058645 1.041027 1.041526 376 2017-04-17 1.019455 1.041021 1.053857 1.073535 1.040673 1.041310 377 2017-04-18 1.021401 1.040732 1.054952 1.073676 1.040310 1.041081 378 2017-04-19 1.023346 1.040444 1.056506 1.075516 1.039928 1.040880 379 2017-04-20 1.025292 1.040155 1.058690 1.077451 1.039515 1.040668 380 2017-04-21 1.027237 1.039866 1.057339 1.076062 1.039111 1.040482 381 2017-04-22 1.029183 1.039577 1.044391 1.063794 1.038662 1.040306 382 2017-04-23 1.031128 1.039288 1.045823 1.065195 1.038245 1.040151 383 2017-04-24 1.033074 1.039000 1.061313 1.079502 1.037819 1.039990 384 2017-04-25 1.035019 1.038711 1.062002 1.081521 1.037425 1.039808 385 2017-04-26 1.036965 1.038422 1.063460 1.082672 1.037037 1.039641 386 2017-04-27 1.038911 1.038133 1.064560 1.084120 1.036612 1.039439 387 2017-04-28 1.040856 1.037844 1.064104 1.083570 1.036158 1.039263 388 2017-04-29 1.042802 1.037555 1.050387 1.070318 1.035691 1.039108 389 2017-04-30 1.044747 1.037267 1.050766 1.070905 1.035266 1.039004 390 2017-05-01 1.046693 1.036978 1.065699 1.085166 1.034845 1.038860 391 2017-05-02 1.048638 1.036689 1.065438 1.085964 1.034422 1.038690 392 2017-05-03 1.050584 1.036400 1.064749 1.085240 1.033968 1.038531 393 2017-05-04 1.052529 1.036111 1.065050 1.085800 1.033469 1.038364 394 2017-05-05 1.054475 1.035823 1.063513 1.083653 1.033025 1.038218 395 2017-05-06 1.056420 1.035534 1.048354 1.067641 1.032520 1.038083 396 2017-05-07 1.058366 1.035245 1.047477 1.066702 1.032109 1.037961 397 2017-05-08 1.060311 1.034956 1.058802 1.081033 1.031638 1.037860 398 2017-05-09 1.062257 1.034667 1.056254 1.078206 1.031123 1.037776 399 2017-05-10 1.064202 1.034379 1.056461 1.077099 1.030642 1.037677 400 2017-05-11 1.066148 1.034090 1.054501 1.076564 1.030145 1.037589 seasonal_lower seasonal_upper weekly weekly_lower weekly_upper yearly 366 0.024767093 0.024767093 0.003940483 0.003940483 0.003940483 0.02082661 367 0.009575525 0.009575525 -0.010410964 -0.010410964 -0.010410964 0.01998649 368 0.008836971 0.008836971 -0.010410964 -0.010410964 -0.010410964 0.01924793 369 0.022674169 0.022674169 0.004035024 0.004035024 0.004035024 0.01863914 370 0.021769561 0.021769561 0.003585140 0.003585140 0.003585140 0.01818442 371 0.022019978 0.022019978 0.004116473 0.004116473 0.004116473 0.01790350 372 0.022955847 0.022955847 0.005144808 0.005144808 0.005144808 0.01781104 373 0.021856639 0.021856639 0.003940483 0.003940483 0.003940483 0.01791616 374 0.007811249 0.007811249 -0.010410964 -0.010410964 -0.010410964 0.01822221 375 0.008315721 0.008315721 -0.010410964 -0.010410964 -0.010410964 0.01872669 376 0.023456231 0.023456231 0.004035024 0.004035024 0.004035024 0.01942121 377 0.023876916 0.023876916 0.003585140 0.003585140 0.003585140 0.02029178 378 0.025435576 0.025435576 0.004116473 0.004116473 0.004116473 0.02131910 379 0.027623915 0.027623915 0.005144808 0.005144808 0.005144808 0.02247911 380 0.027684018 0.027684018 0.003940483 0.003940483 0.003940483 0.02374354 381 0.014669739 0.014669739 -0.010410964 -0.010410964 -0.010410964 0.02508070 382 0.016045356 0.016045356 -0.010410964 -0.010410964 -0.010410964 0.02645632 383 0.031869409 0.031869409 0.004035024 0.004035024 0.004035024 0.02783439 384 0.032763285 0.032763285 0.003585140 0.003585140 0.003585140 0.02917814 385 0.034567524 0.034567524 0.004116473 0.004116473 0.004116473 0.03045105 386 0.036762544 0.036762544 0.005144808 0.005144808 0.005144808 0.03161774 387 0.036585428 0.036585428 0.003940483 0.003940483 0.003940483 0.03264494 388 0.023091454 0.023091454 -0.010410964 -0.010410964 -0.010410964 0.03350242 389 0.023752733 0.023752733 -0.010410964 -0.010410964 -0.010410964 0.03416370 390 0.038641851 0.038641851 0.004035024 0.004035024 0.004035024 0.03460683 391 0.038400090 0.038400090 0.003585140 0.003585140 0.003585140 0.03481495 392 0.038893224 0.038893224 0.004116473 0.004116473 0.004116473 0.03477675 393 0.039631580 0.039631580 0.005144808 0.005144808 0.005144808 0.03448677 394 0.037886050 0.037886050 0.003940483 0.003940483 0.003940483 0.03394557 395 0.022748729 0.022748729 -0.010410964 -0.010410964 -0.010410964 0.03315969 396 0.021730599 0.021730599 -0.010410964 -0.010410964 -0.010410964 0.03214156 397 0.034944144 0.034944144 0.004035024 0.004035024 0.004035024 0.03090912 398 0.033070537 0.033070537 0.003585140 0.003585140 0.003585140 0.02948540 399 0.032014391 0.032014391 0.004116473 0.004116473 0.004116473 0.02789792 400 0.031322816 0.031322816 0.005144808 0.005144808 0.005144808 0.02617801 yearly_lower yearly_upper seasonal yhat 366 0.02082661 0.02082661 0.024767093 1.068676 367 0.01998649 0.01998649 0.009575525 1.053196 368 0.01924793 0.01924793 0.008836971 1.052169 369 0.01863914 0.01863914 0.022674169 1.065717 370 0.01818442 0.01818442 0.021769561 1.064524 371 0.01790350 0.01790350 0.022019978 1.064485 372 0.01781104 0.01781104 0.022955847 1.065132 373 0.01791616 0.01791616 0.021856639 1.063744 374 0.01822221 0.01822221 0.007811249 1.049410 375 0.01872669 0.01872669 0.008315721 1.049626 376 0.01942121 0.01942121 0.023456231 1.064477 377 0.02029178 0.02029178 0.023876916 1.064609 378 0.02131910 0.02131910 0.025435576 1.065879 379 0.02247911 0.02247911 0.027623915 1.067779 380 0.02374354 0.02374354 0.027684018 1.067550 381 0.02508070 0.02508070 0.014669739 1.054247 382 0.02645632 0.02645632 0.016045356 1.055334 383 0.02783439 0.02783439 0.031869409 1.070869 384 0.02917814 0.02917814 0.032763285 1.071474 385 0.03045105 0.03045105 0.034567524 1.072989 386 0.03161774 0.03161774 0.036762544 1.074896 387 0.03264494 0.03264494 0.036585428 1.074430 388 0.03350242 0.03350242 0.023091454 1.060647 389 0.03416370 0.03416370 0.023752733 1.061019 390 0.03460683 0.03460683 0.038641851 1.075620 391 0.03481495 0.03481495 0.038400090 1.075089 392 0.03477675 0.03477675 0.038893224 1.075293 393 0.03448677 0.03448677 0.039631580 1.075743 394 0.03394557 0.03394557 0.037886050 1.073709 395 0.03315969 0.03315969 0.022748729 1.058283 396 0.03214156 0.03214156 0.021730599 1.056976 397 0.03090912 0.03090912 0.034944144 1.069900 398 0.02948540 0.02948540 0.033070537 1.067738 399 0.02789792 0.02789792 0.032014391 1.066393 400 0.02617801 0.02617801 0.031322816 1.065413
Above was the forecast made by Facebook Prophet algorithm. Actual daily closes prices are below.
> tail(data, 35) # A tibble: 35 × 6 Date Open High Low Close Volume <date> <dbl> <dbl> <dbl> <dbl> <int> 1 2017-04-10 1.05881 1.06060 1.05690 1.05953 143236 2 2017-04-11 1.05950 1.06292 1.05778 1.06036 160464 3 2017-04-12 1.06038 1.06742 1.05881 1.06634 177756 4 2017-04-13 1.06626 1.06768 1.06083 1.06133 170756 5 2017-04-14 1.06155 1.06290 1.06052 1.06106 93307 6 2017-04-17 1.06040 1.06697 1.06036 1.06425 61564 7 2017-04-18 1.06417 1.07353 1.06365 1.07294 121388 8 2017-04-19 1.07297 1.07363 1.06990 1.07109 95794 9 2017-04-20 1.07129 1.07768 1.07084 1.07167 101258 10 2017-04-21 1.07159 1.07373 1.06815 1.07068 96497 # ... with 25 more rows
You can compare the predictions with the actual. As said above, if we can predict the market direction correctly, we can use it in our trading strategy to reduce more than 50% of the losing trades. It maybe impossible to predict the price correctly. We should focus more on the market direction. Read the post in which I explain how you can get a free forex VPS on Amazon Web Services.